누적 합(Prefix Sum)
누적 합(Prefix Sum) 알고리즘 (2022 KAKAO BLIND RECRUITMENT 6 파괴되지 않은 건물)
index별 합 구하기
일정 구간[x, y]이 주어지고, 각 배열에서 [x, y]구간이 1일 때, 해당 배열들의 index 값의 합을 구하고자 합니다.
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| array1 | 1 | 1 | 1 | 0 | 0 |
| array2 | 0 | 0 | 1 | 1 | 1 |
| array3 | 0 | 1 | 1 | 1 | 0 |
간단하게 각 index별로 loop를 돌면서 index의 합을 구하면 될 것 같습니다.
python 코드로 구현해본다면 아래와 같을 것입니다.
range1 = [0, 2 +1]
range2 = [2, 4 +1]
range3 = [1, 3 +1]
array1 = [0, 0, 0, 0, 0]
for idx in range(*range1):
array1[idx] = 1
array2 = [0, 0, 0, 0, 0]
for idx in range(*range2):
array2[idx] = 1
array3 = [0, 0, 0, 0, 0]
for idx in range(*range3):
array3[idx] = 1
answer = [0, 0, 0, 0, 0]
for idx in range(5) :
for arr in [array1, array2, array3]:
answer[idx] += arr[idx]
print(answer)
# [1, 2, 3, 2, 1]
답은 찾을 수 있지만, 이러한 구현의 문제점은 이중 루프가 사용되면서 시간복잡도가 증가한다는 것입니다. 주어지는 배열의 개수를 \(N\), 주어지는 배열 중 최대길이를 \(M\)이라고 하면, 시간복잡도는 \(O(NM)\)이 됩니다. 이는 시간 제한을 통과할 수 없는 수준입니다.
\(O(NM)\) 시간복잡도를 \(O(N)\)으로 줄이기
어떻게 하면 \(O(N)\)이라는 시간 안에 배열합을 구할 수 있을까요. 각 배열의 정보를 미리 캐싱해둔다면 가능합니다.
array를 입력받을 때마다, 특정 정보를 기록해둠으로써 이러한 구현이 가능해집니다. 각 배열에서 1이 시작되는 index 그리고 1이 끝나는 index의 다음 index에 1과 -1을 cache에 저장합니다. 즉, 배열에서 값의 시작과 끝만을 기록합니다.
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| array1 | 1 | 1 | 1 | 0 | 0 |
| cache(arr1) | 0+1 | 0 | 0 | 0-1 | 0 |
| array2 | 0 | 0 | 1 | 1 | 1 |
| cache(arr1+arr2) | 1 | 0 | 0+1 | -1 | 0 |
| array3 | 0 | 1 | 1 | 1 | 0 |
| cache(arr1+arr2+arr3) | 1 | 0+1 | 1 | -1 | -1 |
최종적으로 구해진 cache 값을 처음부터 차례대로 더해나가면, 앞의 결과와 같은 결과를 나옵니다.
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| cache | 1 | 1 | 1 | -1 | -1 |
| answer | 1 | 2 | 3 | 2 | 1 |
코드로 구현해보면 아래와 같습니다.
range1 = [0, 2 +1]
range2 = [2, 4 +1]
range3 = [1, 3 +1]
cache = [0, 0, 0, 0, 0]
for start, end in [range1, range2, range3]:
cache[start] = 1
if end > 4 : continue
cache[end] = -1
answer = [0, 0, 0, 0, 0]
answer[0] = cache[0]
for idx in range(1, 5) :
answer[idx] += answer[idx-1] + cache[idx]
print(answer)
# [1, 2, 3, 2, 1]
위와 같이 Prefix를 가지고 계산하는 경우의 시간복잡도는, 각 input으로부터 cache를 만드는 \(O(N)\), 주어진 배열을 index 0부터 더해나가는 과정인 \(O(M)\)입니다. 그리고 이 둘은 루프로 겹치지 않고 각각 따로 계산되므로 최종적으로 시간복잡도는 \(O(N) + O(M)\) 입니다.
이차원 배열에서 누적합의 적용
이러한 원리는 이차원 배열에서도 똑같이 적용됩니다.
예를 들어 5*5 배열에 다음과 같은 배열 2개를 더한다고 합시다.
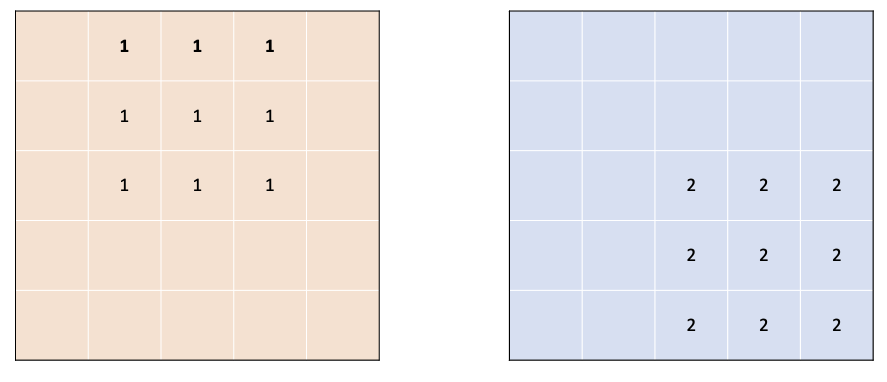
이 경우에 chache는 아래와 같이 만들어집니다.
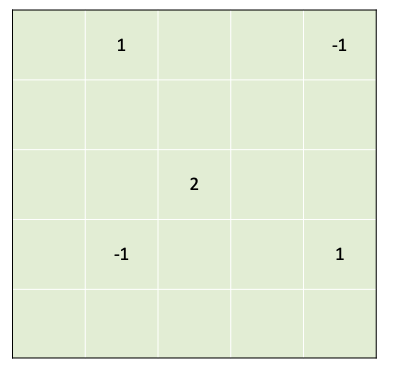
다음은 왼쪽에서 오른쪽, 위에서 아래의 두 번의 합 과정을 수행합니다.
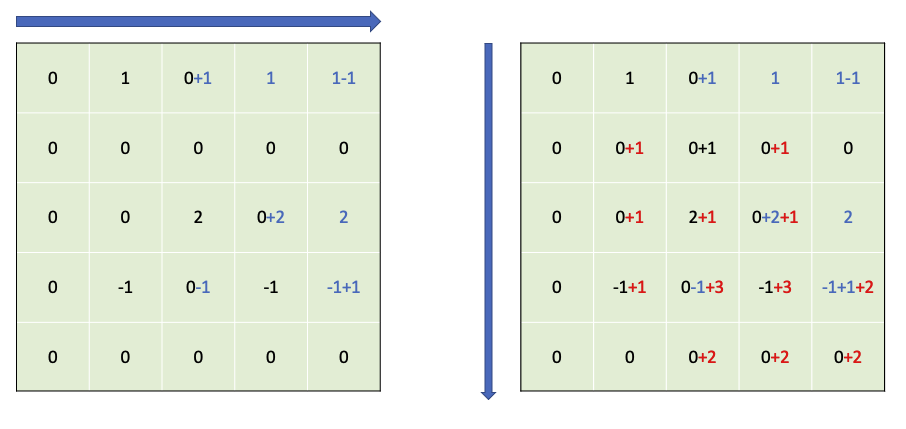
이렇게 수행하게 되면 2차원 배열에서도 부분합 결과를 계산할 수 있습니다.
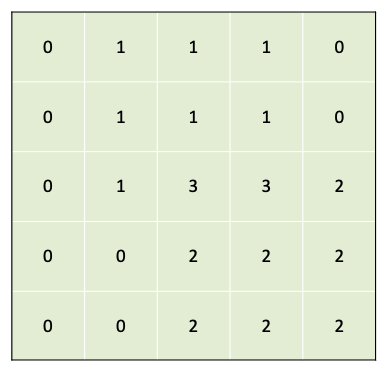
2022 KAKAO BLIND RECRUITMENT 6 파괴되지 않은 건물
2차원 배열에 누적 합을 적용하여 풀이하는 문제였습니다.(https://programmers.co.kr/learn/courses/30/lessons/92344)
풀이 코드는 아래와 같습니다.
def solution(board, skill):
row = len(board)
col = len(board[0])
point_board = [[0 for i in range(col)] for i in range(row)]
for tp, r1, c1, r2, c2, degree in skill :
if tp == 1 :
pm = -1
else : pm = 1
point = pm * degree
rev_point = point * (-1)
# 시작점 좌표
point_board[r1][c1] += point
# 끝점 좌표
if r2+1 < row and c2+1 < col :
point_board[r2+1][c2+1] += point
# y축 종료 알림
if r2+1 < row :
point_board[r2+1][c1] += rev_point
# x축 종료 알림
if c2+1 < col :
point_board[r1][c2+1] += rev_point
# point 누적합 계산
for idx1 in range(row) :
for idx2 in range(1, col) :
point_board[idx1][idx2] += point_board[idx1][idx2-1]
for idx1 in range(1,row) :
for idx2 in range(col) :
point_board[idx1][idx2] += point_board[idx1-1][idx2]
# 기존 점수판에 더하기
for idx1 in range(row) :
for idx2 in range(col) :
board[idx1][idx2] += point_board[idx1][idx2]
# 정답 내기(양수 카운트)
answer = 0
for idx1 in range(row):
for idx2 in range(col) :
if board[idx1][idx2] > 0 :
answer += 1
return answer
좌표계 계산에서 헷갈려서 풀이에 오래 걸렸지만 어찌됬든 정답은 찾아냈습니다!