Softeer 거리 합 구하기
Subtree를 이용한 거리 합 구하기
문제
잘못된 접근 방법 - 모든 노드에서 DFS를 실행
처음 생각해낸 접근은 모든 노드를 시작점으로 하여 DFS를 실행하는 것입니다.
for start_node in range(N) :
dist = dfs(start_node)
print(sum(dist))
이러한 접근은 시간초과를 피할 수 없습니다. 시간복잡도 계산은 다음과 같습니다.
노드의 개수 \(N\), 간선의 개수 \(N-1\)입니다.
DFS의 시간복잡도가 \(O(N+E)\)이므로, 위 문제의 경우에는 \(O(N+N-1)=O(N)\)으로 계산됩니다.
DFS를 \(N\)번 반복하므로 이 경우 시간 복잡도는 \(N*O(N)=O(N^2)\)으로 계산됩니다. \(N≤2*10^5\)인 경우에 \(N^2≤2*10^{10}\) 이기 때문에 시간제한인 2초(Python의 경우 6초) 내에 답을 찾을 수 없습니다.
올바른 접근 - Subtree
What is Subtree?
Tree에서 어떤 한 노드를 Root로 하고, 해댕 노드의 Child로 이루어진 tree를 subtree라고 부릅니다. 이 정의에 따르면 전체 노드를 포함하는 트리(subtree 1a)도 subtree로 정의됩니다.
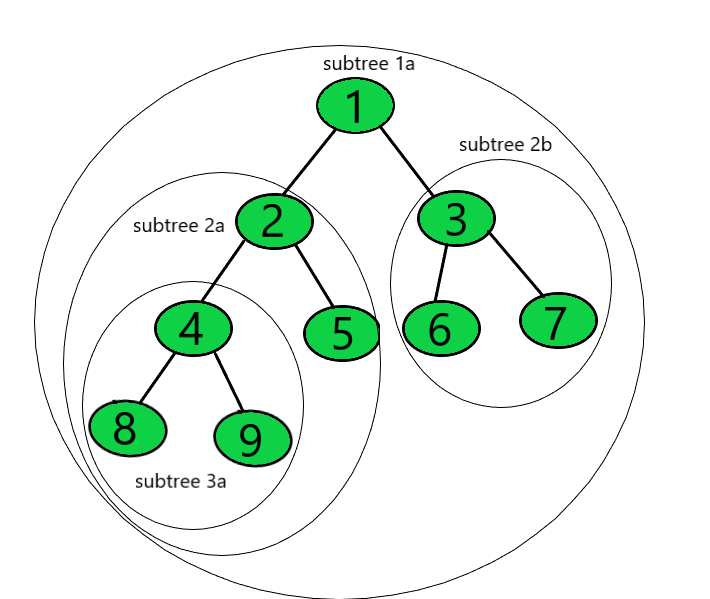
Subtree Size
subtree size란 subtree에 포함된 노드의 개수를 의미합니다. 위 그림에서 subtree size는 아래 표와 같습니다.
| subtree | size |
|---|---|
| 1a | 9 |
| 2b | 3 |
| 2a | 5 |
| 3a | 3 |
subtree 1a의 subtree size는 subtree 2b와 subtree 2a의 subtree size의 합에 1(root node, 1)을 더한 값인 9입니다. 마찬가지로 subtree 2a는 [5] 와 [4,8,9] 로 이루어진 2개 subtree의 size(1, 3)의 합에 1을 더한 값인 5(1+3+1)입니다.
이러한 규칙을 고려해보았을 때, DFS로 노드를 탐색하면서 동시에 각 노드를 root로 하는 subtree size를 구할 수 있습니다.
def dfs(cur, par) :
subSize[cur] = 1 # root node를 반드시 포함하므로 1부터 시작됨
for idx in range(len(nodes[cur])) :
child, weight = nodes[cur][idx]
if child != par :
dfs(child, cur)
subSize[cur] += subSize[child] # cur node의 child의 subtree size를 더해뭄
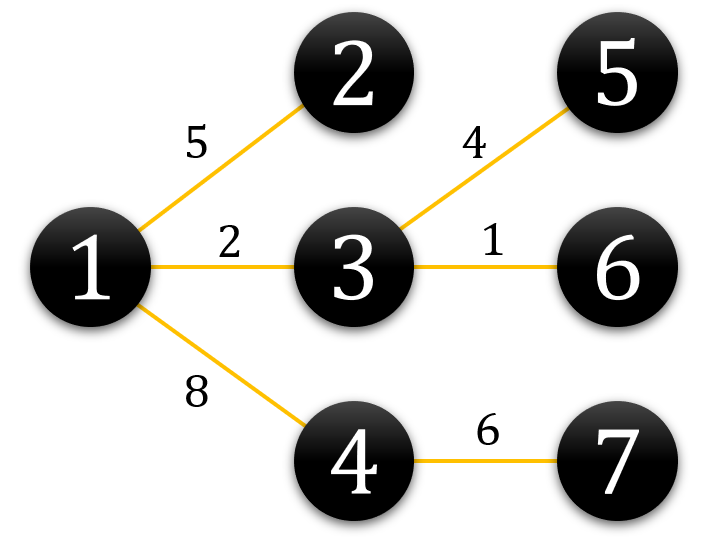
주어진 문제에 대해 subtree size를 구해보면 아래와 같습니다.
| root | subtree size |
|---|---|
| 1 | 7 |
| 2 | 1 |
| 3 | 3 |
| 4 | 2 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
Distance
문제의 예시에서, 1번 노드에서 각 노드 사이의 거리의 합은 아래와 같이 계산됩니다.
| from | to | distance |
|---|---|---|
| 1 | 2 | 5 |
| 1 | 3 | 2 |
| 1 | 4 | 8 |
| 1 | 5 | 6 |
| 1 | 6 | 3 |
| 1 | 7 | 14 |
| 1 | (2,3,4,5,6,7) | 38 |
우리가 구하고자 하는 값은 38이고, 이를 sumDist[1]이라고 정의하겠습니다.
만약 2번 노드에서 각 노드 사이의 거리 합을 구하고자 한다면, 우리는 위에서 계산된 1번 노드에서의 계산 결과를 이용할 수 있습니다.
| from | to | distance | |
|---|---|---|---|
| 2 | 1 | 5 | D(1,2)와 같음 |
| 2 | 3 | 2 + 5 | D(1,3) + D(1,2) |
| 2 | 4 | 8 + 5 | D(1,4) + D(1,2) |
| 2 | 5 | 6 + 5 | D(1,5) + D(1,2) |
| 2 | 6 | 3 + 5 | D(1,6) + D(1,2) |
| 2 | 7 | 14 + 5 | D(1,7) + D(1,2) |
| 2 | (1,3,4,5,6,7) | 38 + 5*(6-1) = 63 | sumDist[1] + D(1,2) * 5 |
3번 노드 역시 마찬가지입니다.
| from | to | distance | |
|---|---|---|---|
| 3 | 1 | 2 | D(1,3)와 같음 |
| 3 | 2 | 5 + 2 | D(2,1) + D(1,3) |
| 3 | 4 | 8 + 2 | D(4,1) + D(1,3) |
| 3 | 5 | 6 - 2 | D(5,1) - D(1,3) |
| 3 | 6 | 3 - 2 | D(6,1) - D(1,3) |
| 3 | 7 | 14 + 2 | D(7,1) + D(1,3) |
| 3 | (1,2,4,5,6,7) | 38 + 2*(3-2) = 40 | sumDist[1] + D(1,2) * 1 |
이러한 계산의 규칙은 각 노드의 subtree size를 이용합니다.
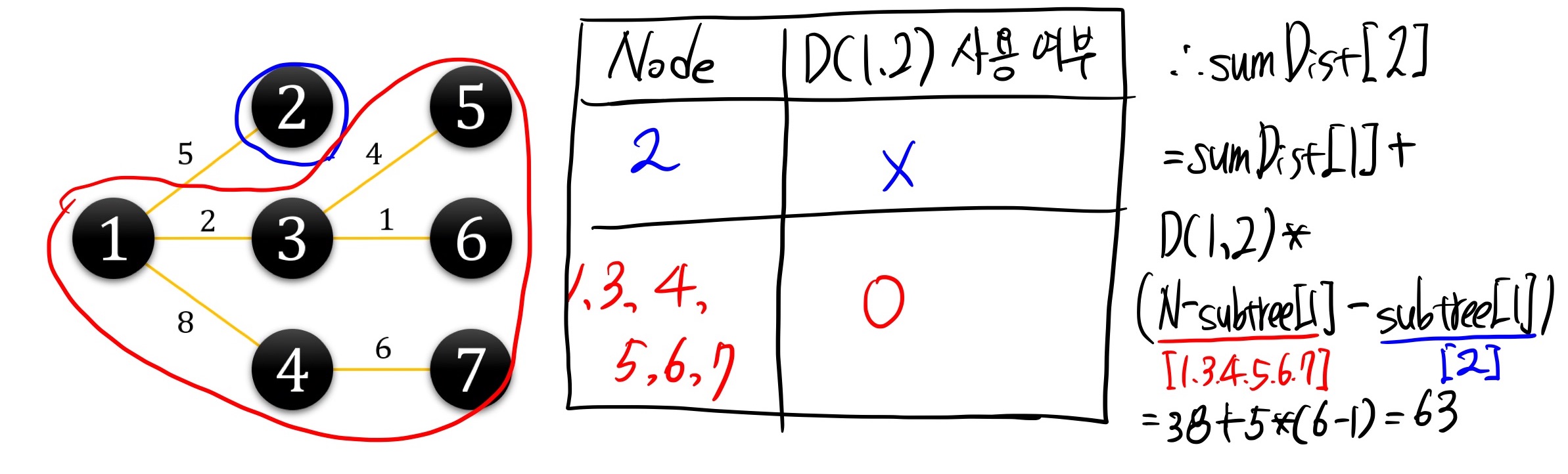
2번 노드는 subtree size가 1이기 때문에(직접 연결된 child가 없기 때문에) 다른 노드와 연결되기 위해서는 부모노드인 1을 반드시 지날 수 밖에 없습니다.
따라서, 2번 노드에서 계산되는 거리합은 1번 노드에서 계산된 거리합에 D(1,2)=5가 항상 추가되고(반드시 D(1,2)를 사용하고) 1번 노드에서는 계산된 값을 그대로 사용합니다.
반대로 3번 노드는 subtree size가 3이기 때문에 2개 노드([5, 6])에 대해서는 직접 접근이 가능하고, 나머지 노드([2,4,7])은 부모노드를 거쳐야합니다. 따라서, [5, 6]에 노드에 대해서는 D(1,3)을 빼주어야하고, [2, 4, 7] 에 대해서는 D(1,3)을 더해줍니다.
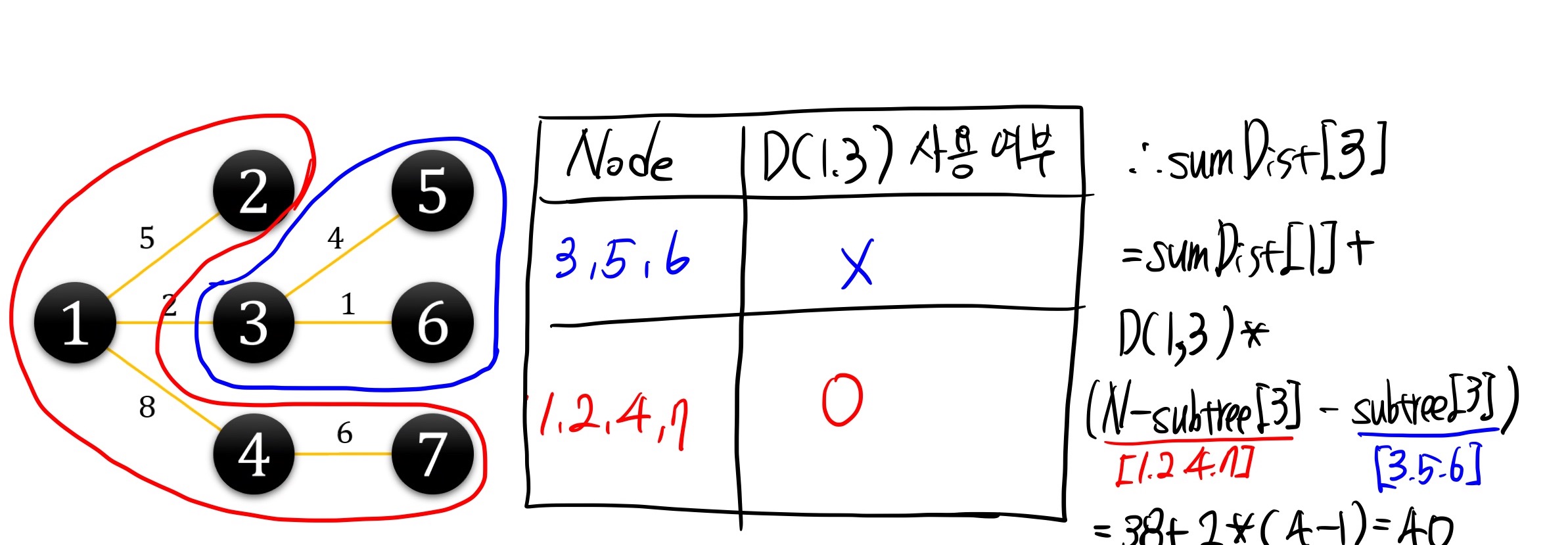
이러한 계산을 위해서는 DFS 탐색을 한번 더 수행해야합니다.
Answer
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
N = int(input())
nodes = [[] for i in range(N+1)]
for _ in range(N-1):
x, y, t = map(int, input().split())
nodes[x].append((y, t))
nodes[y].append((x, t))
# 1번 노드를 기준으로는 똑같이 계산한다
# 1과 인접한 노드에 대해서는 상수 시간에 구한다
# 이를 위해 subtree size가 필요하다
# subtree size란 ? 어떤 노드를 root로 했을 때, 본인을 포함한 노드 개수는 ?
# 2번 노드를 기준으로 생각했을 때,
# 나머지 6개 노드에 대해서 1번을 거쳐서 2번으로 들어오므로, D(1,2) = 5 만큼 증가한다
# 2의 subtree들은 5가 감소한다
subSize = [0 for i in range(N+1)]
dist = [0 for i in range(N+1)]
def dfs(cur, par) :
subSize[cur] = 1
for idx in range(len(nodes[cur])) :
child, weight = nodes[cur][idx]
if child != par :
dfs(child, cur)
dist[cur] += subSize[child] * weight + dist[child]
subSize[cur] += subSize[child]
def dfs2(cur, par) :
for idx in range(len(nodes[cur])):
child, weight = nodes[cur][idx]
if child != par :
dist[child] = dist[cur] + weight * (N-subSize[child]-subSize[child])
dfs2(child, cur)
dfs(1,1)
dfs2(1,1)
for idx in range(1, N+1) :
print(dist[idx])
결국 DFS를 2번 수행하므로 시간복잡도는 \(2*O(N+E)\)이고 위 문제에서는 \(O(N)\)의 시간복잡도로 정답을 찾을 수 있습니다.
[참고]